This is one of the mathematical equation-based questions where variables and numbers are given. 4x ^ 2 – 5x – 12 = 0 is an example of a quadratic equation. This equation is a mathematical equation and it requires a formula to solve it.
This equation will test your mathematical knowledge and abilities. Such forms of mathematics improve ours thinking ability. This type of quadratic equations problem is generally solved by simplification method. Simplification method means breaking of equations till it equalizes the equation. In this equation.
About Quadratic Equation: 4x ^ 2 – 5x – 12 = 0
4x ^ 2 – 5x – 12 = 0 is a problem-based equation that is asked to be solve to prove a solution. We have to prove that left hand side is equal to right hand side (L.H.S = R.H.S). Mathematical equations are just seemed to be complex but they’re actually difficult.
Quadratic equation is a mathematical term. The given equation is a prime example of quadratic equation. Quadratic equations are represented in the form of ax^2 + bx + c = 0.
- Example: In the given equation, ax^2 + bx + c = 0. The term a, b, c are known as coefficient, a is not equal 0. The term ‘x’ is represented as variable.
Formula to solve:- 4x2 – 5x – 12 = 0
The given equation is a quadratic expression. It requires a specific formulas to solve such the world of mathematical expressions which is given below.
Quadratic Formula:–

Through the above formula we can easily calculate the method to solve the given equation 4x ^ 2 – 5x – 12 = 0.
This formula is a formula of simplification in which we simplify the equation as much as possible. Al-Khwarizmi gave this formula to solve all the equations to its simplest form.
Solution By Using The Above Quadratic Formula
On simply adding all the respective values in this formula we can find a right solution.
We will solve the equation by quadratic formula.
Quadratic formula:

In this given equation: a = 4, b = – 5 and c = – 12 where a is not equal to 0. The term ‘x’ is an unknown factor.
To solve the given problem we need to place the values of coefficient on the quadratic formula.
Assume, X = x
- X = [ -b ± √ (b2 – 4ac)] / 2a
- X = [ – (-5) ± √ ( (-5)2– 4 (4) (-12))] / 2 (4)
- X = [ 5 ± √ ( 25 +192 )] / 8
- X = 5 + √ 217 / 8 and X = 5 – √ 217 / 8
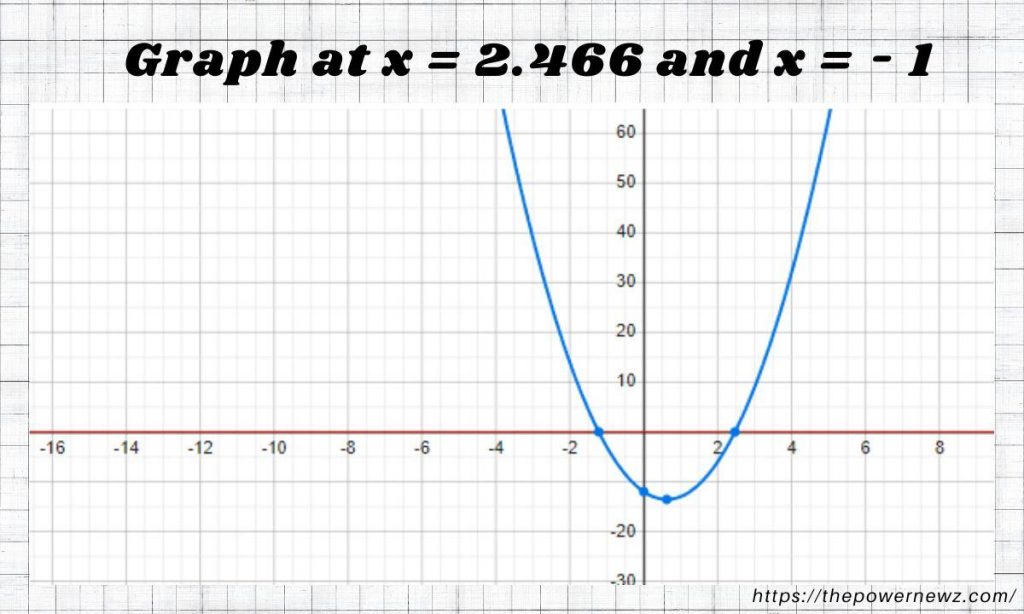
Thus, we got the solution where, x = 2.466 and x = – 1.216
Graph x = 2.466 and x = – 1.216
Techniques to Solve 4x ^ 2 – 5x – 12 = 0
Completing the square
Divide the equation by the coefficient of square variable. It means divide the equation by the coefficient ‘a’ then imply the square method. Add a constant term on both the sides of the equation and calculate.
Factoring
Factoring is a technique to solve an equation by splitting the middle terms of the equation. Factoring technique is used to determine the factors of an equation and then it is solved.
Taking the Square Root
In this technique we have separated the square terms and the constant term opposite to each other. Square root out is a method to find a solution for solving Quadratic Equation. In this technique we solve the roots of both the sides to get an accurate answer for this.
Explain:- Why coefficient ‘a’ is not equal to zero in a quadratic equation?
If the coefficient ‘a’ is represented with value 0 then it will change the whole form of equation. It will get converted to a linear equation from the quadratic equation.
It is a theory that coefficient ‘a’ can never be represented with a value 0 or else will never find a solution. Mathematics have rules and regulations for each mathematical concept.
Conclusion
Mathematics is a game of formula, if you know the formula you can crack all the mathematical problems. Quadratic equations are very easy to solve when we apply the right formula. If we have the formula, we have just put the right value at the right position and it’s done.
4x ^ 2 – 5x – 12 = 0 equation can be solve by four different methods. In the equation can be asked in the format of multiple choice questions also. By breaking down the value of ‘x’ we have found the right solution for the term.
To find the solution for the above listed three equations, same quadratic formula is used to find the value of ‘x’. Mathematics just looks difficult but it’s not a difficult subject. Quadratic equations is a small universe in the cosmos of mathematics.
Also, Read About:-
